The most fundamental form of the existence of matter in the Universe - the space-time continuum - has a set of properties that determine the face of our world and the general nature of the processes occurring in it. Among these fundamental categories are the homogeneity and isotropy of space. These are the properties from which, as we will see below, the most important consequences for the knowledge of the Universe follow.
The concept of homogeneity and isotropy
Homogeneity means the absence of selected points in space. All locations are the same and equal in relation to the action of the laws of nature, and the latter do not change during the transition (translation) from one point to another. That is, in the space of the Universe the same laws apply throughout its entire length, and the parallel transfer of any closed physical system will not affect its functioning in any way.
The isotropy of space is the absence of distinguished, special directions in it. No matter what orientation in space we choose, no matter what angle the reference system is rotated, the laws of nature will not change their effect - all directions are equal. No change in the orientation of a closed system can affect its properties.
Space and Time in Newtonian Physics
The homogeneity and isotropy of space are key concepts in the classical mechanics of Galileo and Newton. The space in the framework of this teaching was thought to be infinite, flat, homogeneous, isotropic and absolute, that is, completely indifferent to the distribution of matter in it. The space was supposed to exist only as a kind of place where physical bodies are located, interacting with each other - but not with their "container". Such a space could serve as an ideal, inertial reference frame independent of nothing.
As for time, his Newtonian concept defines time as well as a kind of independent, absolute category, referring exclusively to the duration of various processes. Time in the Newtonian understanding is uniform and synchronous for the entire Universe, it is separated from matter, from moving bodies.
About the properties of time
It is necessary to say a few words about time. Since time is one-dimensional, it can have two equal directions - this would mean its complete reversibility, and hence the absolute isotropy of both space and time. However, with some special exceptions related to phenomena in the world of elementary particles, we do not observe reversible processes in nature. The Universe is evolving in one direction, given by the so-called “arrow of time”. This concept is connected with the thermodynamics of the Universe as a closed system, which had certain initial conditions for development.
Time, therefore, being homogeneous, since it does not have selected moments (all points on the time axis are equal), is not isotropic.
Homogeneity and isotropy of space-time
The special theory of relativity has shown that space and time are not absolute and not separated from each other, but are closely interrelated categories involved in the movement of matter. Space-time is a four-dimensional continuum - a topological manifold, the points of which are not locations and moments separately and independently from each other, but events defined by four coordinates in a specific reference frame.
The general theory of relativity supplemented the concept of space-time, considering it as an object closely related to the distribution and behavior of moving masses of matter - matter and fields. It may seem that such an understanding contradicts the thesis of the isotropy of space. This, however, is not so. There are no distinguished events in the four-dimensional continuum, all of them are equal in relation to the laws of nature, therefore space-time is homogeneous. In a sense, one can speak of the peculiar isotropy of the continuum, since time in it is closely linked with space. But the thermodynamic “arrow of time” imposes a very strict (albeit probabilistic in nature) restriction on the isotropy of time.
Isotropy as a manifestation of symmetry
As well as homogeneity, the isotropy of space is a reflection of symmetry, a fundamental property inherent in the basic laws of the universe. Symmetry, or invariance in the broad, physical sense, means that the parameters characterizing the system do not change after the system undergoes certain transformations. Thus, homogeneity is a manifestation of translational symmetry.
There is also rotational invariance, or rotation symmetry, to which space obeys. It is it that manifests itself in the form of isotropy.
Symmetry and conservation laws
All symmetries are associated with laws (sometimes they even speak of principles - universal laws) of conservation. For example, the uniformity of time, that is, independence from the moment at which the physical system exists, entails the principle of conservation of energy, the homogeneity of space - the law of conservation of momentum (momentum).
A consequence of the isotropy of space is the law of conservation of angular momentum (angular or kinetic moment). This means that the amount of rotational motion of a closed system is indifferent to the angle of its rotation relative to any selected axis. You can also talk about the rectilinear movement of the system past an arbitrary point. Relative to it, our system also has an angular momentum.
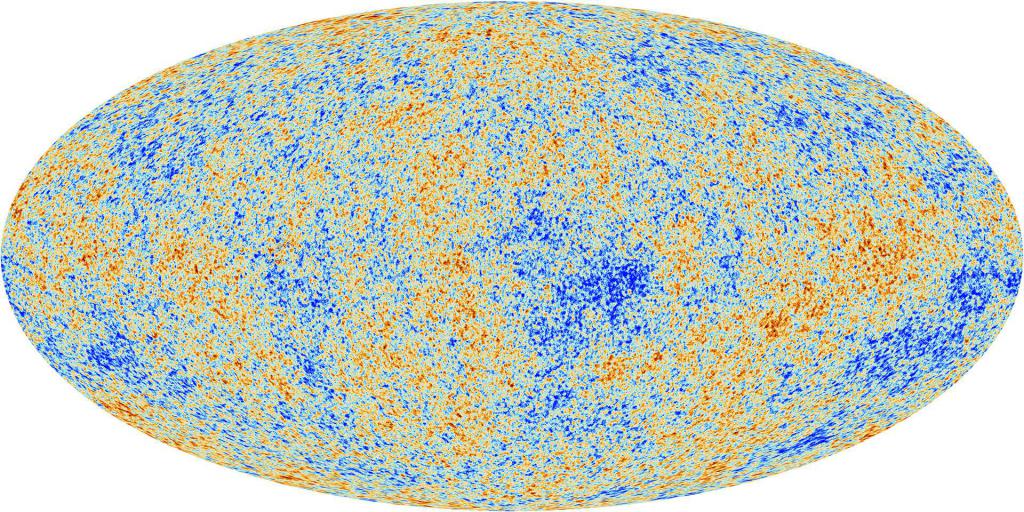
The often perplexing concern about isotropy (and homogeneity) is usually caused by the fact that, observing the Universe on any scale, we see that the matter is distributed and moves in it extremely inhomogeneously at different points and in different directions. To dispel bewilderment, it is enough to imagine that the distant galaxy has moved or that we have removed the vase from the table - after all, after that, the laws of physics in that direction did not cease to be fulfilled. In the same way, they will work regardless of whether the car passes by the house or at what height and in what plane the satellite’s orbit is located.