Arrow's impossibility theorem and its effectiveness

The paradox of the theory of public choice was first described by the Marquis of Condorcet in 1785, which was successfully generalized by the American scientist economist C. Arrow in the 1950s. Arrow's theorem answers a very simple question in collective decision theory. Let's say there are several options for choosing in matters of politics, public projects or income distribution and there are people whose preferences determine this choice.

The question is what procedures exist for the qualitative determination of a choice. And how to learn about preferences, about the collective or social ordering of alternatives, from best to worst. Arrow's answer to this question surprised many.

Arrow’s theorem says that there are no such procedures at all - in any case, they do not meet certain and quite reasonable preferences of people. The technical structure in which Arrow gave a clear meaning to the problem of social order, and his rigorous answer are now widely used to study problems in the social economy. The theorem itself formed the basis of the modern theory of public choice.

Theory of Public Choice

Arrow's theorem shows that if voters have at least three alternatives, then there is no electoral system that could transform the choice of individuals into public opinion.

The shocking statement came from economist and Nobel laureate Kenneth Joseph Arrow, who demonstrated this paradox in his doctoral dissertation and popularized it in the book Social Choice and Individual Values, published in 1951. The original article is entitled "Difficulties in the Concept of Social Security."

Arrow’s theorem says that it’s impossible to develop an electoral system with an order that always meets fair criteria:

1. When a voter chooses an alternative X versus Y, then the community of voters will choose X rather than Y. If the choices for each of the voters X and Y remain unchanged, then the choice of society X and Y will be the same even if voters choose other pairs X and Z , Y and Z or Z and W.
2. There is no “choice dictator," because one voter cannot influence the choice of a group.
3. Existing electoral systems do not cover the required requirements, as they provide more information than the rank.

State social management systems

Although the American economist Kenneth Arrow received the Nobel Prize in economics, the work did more good for the development of social sciences, since Arrow’s theorem on impossibility laid the foundation for a completely new direction in economics - social choice. This industry is trying to mathematically analyze the adoption of joint decisions, in particular in the field of public social management systems.

Choice is democracy in action. People go to the polls and express their preferences, and as a result, the preferences of many people must come together to make a joint decision. That is why the choice of voting method is very important. But is there a perfect vote in reality? According to the results of Arrow's theory, obtained in 1950, the answer is no. If “ideal” means a preferential voting method that meets the criteria of certain reasonable voting methods.

The preferred voting method is ranking, when voters evaluate all candidates in accordance with preferences, and based on these ratings, the result is obtained: another list of all candidates that should be represented by the general will of people. By Arrow’s Impossibility Theorem, you can specify a reasonable voting method:

1. Without dictators (ND) - the result does not always have to coincide with the assessment of one particular person.
2. Pareto Efficiency (PE) - if each voter prefers candidate A to candidate B, then the result should indicate candidate A over candidate B.
3. Independence of Incompatible Alternatives (IIA) is a relative assessment of the results of candidates A, B and should not be changed if voters change the assessment of other candidates but do not change their relative ratings of A and B.

According to the conditions of Arrow's theorem, it turns out that in the case of elections with three or more criteria, there are no social choice functions that would be simultaneously suitable for ND, PE, and IIA.

Rational choice system

The need for aggregation of preferences is manifested in many areas of human activity:

1. The welfare economy uses microeconomic methods to measure welfare at the aggregate overall economic level. A typical methodology begins with the derivation or assumption of a social security function, which can then be used to rank economically sound resource allocations in terms of social security. In this case, states are trying to find an economically acceptable and stable result.
2. In decision theory, when a person must make a rational choice according to several criteria.
3. In electoral systems, which are mechanisms to find a single solution from the preferences of many voters.

According to the conditions of Arrow's theorem, the order of preferences for a given set of parameters (results) is distinguished. Each unit in a society or each decision-making criterion assigns a certain order of preferences regarding a set of results. The company is looking for a rating-based voting system called the social security function.

This preference aggregation rule converts a preference profile set into one global public order. Arrow’s statement says that if the governing body has at least two voters and three selection criteria, it is impossible to create a social security function that will satisfy all these conditions at once.

For each set of individual preferences of voters, the social security function must fulfill a unique and comprehensive rating of public selection:

1. This should be done in such a way that the result is a complete assessment of the preferences of the audience.
2. Must deterministically give the same score when voters' preferences seem the same.

Independence from irrelevant alternatives (IIA)

The choice between X and Y is exclusively related to the individual’s preferences between X and Y - this is independence in pairs (pairwise independence), according to Arrow’s theorem on the impossibility of democracy. Moreover, a change in a person’s assessment of irrelevant alternatives located outside such groups does not affect the social assessment of this subset. For example, the representation of a third candidate in an election with two candidates does not affect the election result unless the third candidate wins.

Society is characterized by uniformity and a positive combination of social and individual values. If a person changes his order of preferences, promoting a certain option, then the order of preferences of society should correspond to the same option without changing. A person should not be able to harm an option by rating it higher.

In the theorem on impossibility, efficiency and justice in society are ensured through the sovereignty of the citizen. Every possible social order of preferences should be achievable with a certain set of individual orders of preference. This means that the social security function is surjective - it has unlimited target space. A later (1963) version of Arrow's theorem replaced the criteria for monotony and lack of overlap.

Pareto. Efficiency or unanimity?

If each person prefers a certain option to another, then the order of social preferences should also do this. It is essential that the social security function is minimally sensitive to the profile of preferences. This later version is more general and has somewhat weak conditions. Axioms of uniformity, the absence of overlap with IIA, indicate Pareto effectiveness. At the same time, it does not imply the imposition of IIA and does not imply monotony.

IIA has three goals:

1. Standard. Irrelevant alternatives should not matter.
2. Practical Use of minimal information.
3. Strategic. Providing the right incentives to truly identify individual preferences. Although the strategic objective is conceptually different from IIA, they are closely related.

Pareto efficiency, named after the Italian economist and political scientist Wilfredo Pareto (1848-1923), is used in the neoclassical economy along with the theoretical concept of perfect competition as a guideline for assessing the effectiveness of real markets. It should be noted that not one of the results is achieved beyond the boundaries of economic theory. Hypothetically, if there were perfect competition and resources were used with maximum efficiency, then everyone would have the highest standard of living, or Pareto efficiency.

In practice, it is impossible to take any social actions, such as changing economic policies, without worsening the situation of at least one person, so the concept of Pareto improvement has found wider application in the economy. Pareto improvement occurs when a change in distribution does not harm anyone and helps at least one person, given the initial distribution of goods for a group of people. The theory suggests that Pareto improvements will continue to add value to the economy until a Pareto equilibrium is reached, when no further improvements can be made.

A formal statement of the theorem

Let A be a set of results, N by the number of voters or decision criteria. Denote the set of all complete linear orderings from A to L (A). The strict social security function (preference aggregation rule) is a function that aggregates voters' preferences in a one-time preference order on A.

N is a tuple (R 1, ..., RN) ∈ L (A) N voters preferences is called a preference profile. In its strongest and simplest form, Arrow's impossibility theorem states that whenever a set of possible alternatives A has more than 2 elements, the following three conditions become incompatible:

1. Unanimity, or poor Pareto efficiency. If alternative A is ranked strictly above B for all orders of R 1, ..., RN, then A is ranked strictly above B by F (R 1, R 2, ..., RN). Moreover, unanimity implies the absence of imposition.
2. Non-dictatorship. There is no individual "I" whose strict preferences always prevail. That is, there is no I ∈ {1, ..., N} that for all (R 1, ..., RN) ∈ L (A) H, it takes strictly higher than B from R. The "I" takes strictly higher than B in F (R 1, R 2, ..., RN), for all A and B.
3. Independence from irrelevant alternatives. For two preference profiles (R 1, ..., RN) and (S 1, ..., SN), such that for all individuals I, alternatives A and B have the same order in R i as in S i, alternatives A and B, have the same order in F (R 1, R 2, ..., RN) as in F (S 1, S2, ..., SN).

Interpretation of the theorem

Although the impossibility theorem is proved mathematically, it is often expressed non-mathematical way by stating that none of the voting methods is fair, each ranked voting method has flaws, or the only voting method that is not erroneous is dictatorship. These statements are a simplification of Arrow's result, which is not always considered true. Arrow's theorem states that the deterministic mechanism of pre-emptive voting, that is, the one in which the order of preferences is the only information when voting, and any possible set of votes gives a unique result, cannot simultaneously meet all the conditions mentioned above.

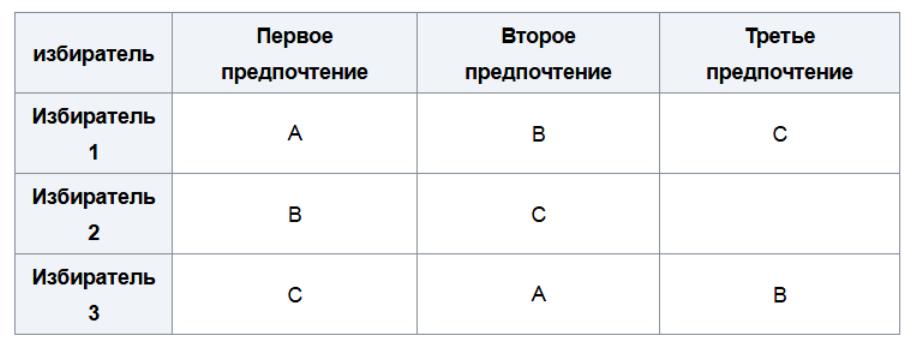
Various theorists have proposed loosening criterion IIA as a way out of the paradox. Proponents of rating methods of voting argue that the IIA is an unreasonably strong criterion, which is violated in most useful electoral systems. Proponents of this position indicate that non-compliance with standard IIA criteria is trivially implied by the possibility of cyclical preferences. If voters vote as follows:

• 1 vote for A> B> C;
• 1 vote for B> C> A;
• 1 vote for C> A> B.

Then the preference of the group in the doubles majority is that A wins over B, B wins over C, and C wins over A and this gives preference to “scissors-rock-scissors” for any pair comparison.

In this case, any aggregation rule that satisfies the basic majority requirement that the candidate with the most votes must win the election will not meet criterion IIA if social preferences should be transitive or acyclic. To see this, it is suggested that such a rule satisfies IIA. Since most preferences are respected, society prefers A - B (two votes for A> B and one for B> A), B - C and C - A. Thus, a cycle is created that contradicts the assumption that social preferences are transitive .

So, Arrow’s theorem really shows that any electoral system with most victories is a non-trivial game, and that game theory should be used to predict the outcome of most voting mechanisms. This can be considered as a discouraging result, because the game should not have effective equilibria, for example, voting can lead to an alternative that no one really wanted, but everyone voted for it.

Social choice instead of preference

The rational collective choice of the voting mechanism according to Arrow's theorem is not the goal of making social decisions. Often enough to find some alternative. An alternative-focused approach explores either social choice functions that display each preference profile or social choice rules — functions that map each preference profile into a subset of alternatives.

As for the functions of social choice, the Gibbard-Satterweit theorem is well known, which states that if the function of social choice, the range of which contains at least three alternatives, is strategically stable, then it is dictatorial. Considering the rules of social choice, they consider that social preferences are behind them.

That is, they consider the rule as the choice of maximum elements - the best alternatives to any social preference. Many of the maximum elements of social preference are called the core. The conditions for the existence of an alternative in the core were investigated in two approaches. The first approach assumes that preferences are at least acyclic, which is necessary and sufficient for preferences to have a maximum element in any finite subset.

For this reason, it is closely related to relaxing transitivity. The second approach rejects the assumption of acyclic preferences. Kumabe and Mihara have taken this approach. They made a more consistent assumption that individual preferences are of maximum importance.

Relative risk aversion

There are several indicators of risk aversion expressed by the utility function in Arrow Pratt's theorem. Absolute risk aversion - the higher the curvature u (c), the higher the risk aversion. However, since the expected utility functions are not uniquely defined, a measure is needed that remains constant with respect to these transformations. One such measure is the Arrow-Pratt measure of absolute risk aversion (ARA), after economists Kenneth Arrow and John W. Pratt determined the coefficient of absolute risk aversion as

A (c) = - {u '' (c)} / {u '(c)},

where: u '(c) and u' '(c) denote the first and second derivatives with respect to "c" from "u (c)".

Experimental and empirical data mainly correspond to a decrease in absolute risk aversion. The measure of relative risk aversion Arrow Pratt (ACP) or the coefficient of relative risk aversion is determined by:

R (c) = cA (c) = {-cu '' (c)} / {u '(c) R (c).

As in the case of absolute risk aversion, the relevant terms are used: constant relative risk aversion (CRRA) and decrease / increase in relative risk aversion (DRRA / IRRA). , , , / «c». RRA ARA , . , : u (c) = log (c), RRA = 1.

: , , , , , . - , . - 1 2 , , , , .

, , , , , . « » , , . , , , , , .

Practical applications of the theorem are used to evaluate wide categories of voting systems. Arrow's main argument is that voting systems should always violate at least one of the criteria of justice that he outlined. The practical consequence of this is that voting systems that are not put in order should be studied. For example, rating voting systems where voters give each candidate points can meet all Arrow criteria.

In fact, the voting mechanism, rational collective choice by Arrow's Theorem and the subsequent dialogue, were incredibly misleading in the electoral field. Often, students and non-specialists believe that no voting system can meet Arrow's fairness criteria, while, in fact, rating systems are able to meet and satisfy all Arrow's criteria.