The binary search tree is a structured database containing nodes, two links to other nodes, on the right and left. Nodes are an object of a class that has data, and NULL is a sign denoting the end of a tree.
It is often referred to as BST, which has a special property: nodes larger than the root are located to the right of it, and smaller ones to the left.
General Theory and Terminology
In a binary search tree, each node, except the root, is connected by a directed edge from one node to another, which is called the parent. Each of them can be connected to an arbitrary number of nodes, called child nodes. Nodes without “children” are called leaves (external nodes). Elements that are not leaves are called internal. Nodes with the same parent are brothers and sisters. The topmost node is called the root. The BST assigns an element to each node and makes sure that they have a special property.
Tree terminology:
- The depth of the node is the number of edges defined from the root to it.
- The height of the knot is the number of edges defined from it to the deepest sheet.
- The height of the tree is determined by the height of the root.
- The binary search tree is a special design, it provides the best ratio of height and number of nodes.
- Height h with N nodes no more than O (log N).
This can be easily proved by counting the nodes at each level, starting from the root, assuming that it contains the largest number of them: n = 1 + 2 + 4 + ... + 2 h-1 + 2 h = 2 h + 1 - 1 Solving this with respect to h, we obtain h = O (log n).
Wood Benefits:
- Reflect structural data relationships.
- Used to represent hierarchies.
- Provide efficient installation and search.
- Trees are very flexible data, allowing you to move subtrees with minimal effort.
Search method
In general, to determine if this value is in the BST, start the binary search tree from its root and determine whether it meets the requirements:
- be at the root;
- be in the left root subtree;
- in the right subtree of root.
If no base register is executed, a recursive search is performed in the corresponding subtree. There are actually two basic options:
- The tree is empty - return false.
- The value is in the root node - return true.
It should be noted that a binary search tree with a developed scheme starts the search always along the path from the root to the leaf. In the worst case, it goes all the way to the leaf. Therefore, the worst time is proportional to the length of the longest path from root to leaf, which is the height of the tree. In general, this is when you need to know how long it takes to search as a function of the number of values stored in the tree.
In other words, there is a relationship between the number of nodes in the BST and the height of the tree, depending on its “shape”. In the worst case, nodes have only one child, and a balanced binary search tree is essentially a linked list. For example:
fifty
/
10
\
fifteen
\
thirty
/
twenty
This tree has 5 nodes and height = 5. To search for values in the range 16–19 and 21–29, the next path from the root to the leaf (a node containing a value of 20) will be required, that is, it will take time proportional to the number of nodes. At best, they all have 2 children, and the leaves are located at the same depth.
This binary search tree has 7 nodes and height = 3. In general, a tree like this (full tree) will have a height of approximately log 2 (N), where N is the number of nodes in the tree. The value of log 2 (N) is the number of times (2) when you can divide N before it reaches zero.
To summarize: the worst time it takes to search in BST is O (tree height). In the worst case, the “linear” tree is O (N), where N is the number of nodes in the tree. In the best case, the “complete” tree is O (log N).
BST Binary Insert
When wondering where the new node should be located in BST, you need to understand the logic, it should be placed where the user finds it. In addition, you need to remember the rules:
- Duplicates are not allowed; an attempt to insert a duplicate value will throw an exception.
- The public insert method uses the helper recursive helper method to actually insert.
- The node containing the new value is always inserted as a sheet in the BST.
- The public insert method returns void, but the helper method returns BSTnode. He does this to handle the case where the node passed to him is zero.
In the general case, a helper method indicates that if the original binary search tree is empty, the result is a tree with one node. Otherwise, the result will be a pointer to the same node that was passed as an argument.
Delete in binary algorithm
As one would expect, deleting an element is related to finding a node that contains the value that needs to be deleted. There are several things in this code:
- BST uses a helper, overloaded delete method. If the item to be searched is not in the tree, then the helper method will be called with n == null. This is not considered a mistake, the tree in this case simply does not change. The auxiliary deletion method returns a value - a pointer to the updated tree.
- When a sheet is deleted, when it is deleted from the binary search tree, the corresponding child pointer of its parent is set to zero or the root to null if the node to be deleted is the root and it has no children.
- It should be noted that the call for deletion must be one of the following: root = delete (root, key), n.setLeft (delete (n.getLeft (), key)), n.setRight (delete (n.getRight (), key)). Thus, in all three cases, it is correct when the delete method simply returns null.
- When the search for the node containing the deleted value is completed successfully, there are three options: the node to delete is a sheet (has no children), the deleted node has one child, it has two children.
- When the node to be deleted has one child, you can simply replace it with a child, returning a pointer to the child.
- If the node to be deleted has zero or 1 child, then the delete method will “follow the path” from the root to this node. Thus, the worst time is proportional to the height of the tree, both for search and insertion.
If the node to be deleted has two children, the following steps are performed:
- Find the node to be deleted by following the path from the root to it.
- Find the smallest value of v in the right subtree while continuing to move along the path to the sheet.
- Recursively delete the value of v, follow the same path as in paragraph 2.
- Thus, in the worst case, the path from the root to the leaf is performed twice.
Traverse order
Traversal is a process that visits all nodes in a tree. Since the binary search tree C is a nonlinear data structure, a unique crawl does not exist. For example, sometimes several bypass algorithms are grouped into the following two types:
- depth crossing;
- first pass.
There is only one type of width intersection - level traversal. This bypass visits nodes down and left, top and right.
There are three different types of depth crossings:
- Walkthrough PreOrder - First visit the parent and then the left and right child.
- InOrder walkthrough - visiting the left child, then the parent and the right child.
- PostOrder workaround - visiting the left child, then the right child, and then the parent.
An example for four traversals of a binary search tree:
- PreOrder - 8, 5, 9, 7, 1, 12, 2, 4, 11, 3.
- InOrder - 9, 5, 1, 7, 2, 12, 8, 4, 3, 11.
- PostOrder - 9, 1, 2, 12, 7, 5, 3, 11, 4, 8.
- LevelOrder - 8, 5, 4, 9, 7, 11, 1, 12, 3, 2.
The figure shows the order of visits to nodes. The number 1 indicates the first node in a particular round, and 7 indicates the last node.
These common workarounds can be represented as a single algorithm, assuming that each node is visited three times. Euler tour is a walk around a binary tree, where each edge is seen as a wall that the user cannot cross. In this walk, each node will be visited either on the left, or below, or on the right. The Euler tour, in which the nodes to the left are visited, causes a preposition to be bypassed. When the nodes below are visited, they get a crawl in order. And when the nodes are visited on the right, they get a surgical bypass.
Navigation and debugging
To facilitate the movement of the tree, create functions that pre-check whether they are a left or right child. To change the position of a node, there must be easy access to the pointer in the parent node. Implementing a tree correctly is very difficult, so you need to know and apply debugging processes. In a binary search tree with implementation, there are often pointers that do not actually indicate the direction of travel.
To understand all this, a function is used that checks whether the tree can be correct and helps to find many errors. For example, checks if the parent node is a child node. With assert (is_wellformed (root)), many errors can be caught prematurely. Using a pair of defined control points inside this function, you can also determine exactly which pointer is wrong.
Konsolenausgabe Function
This function completely resets the tree to the console and is therefore very useful. The order of fulfillment of the goal of the tree output:
- To do this, you first need to determine what information will be displayed through the node.
- And you also need to know how wide and tall the tree is to take into account how much free space you need to leave.
- The following functions calculate this information for the tree and each subtree. Since you can write to the console only line by line, you will also need to display the tree line by line.
- Now we need a different way to output the whole tree, and not just line by line.
- Using the dump function, you can read the tree and significantly improve the output algorithm, since it concerns speed.
However, this feature will be difficult to use on large trees.
Copy constructor and destructor
Since the tree is not a trivial data structure, it is better to implement the copy constructor, destructor, and assignment operator. A destructor is easy to implement recursively. For very large trees, it can handle heap overflows. In this case, it is formulated iteratively. The idea is to remove the leaf representing the smallest value of all the leaves, so it is on the left side of the tree. Cutting off the first leaves creates new ones, and the tree shrinks until it finally ceases to exist.
The copy constructor can also be implemented recursively, but care must be taken if an exception is thrown. Otherwise, the tree quickly becomes confused and error prone. That's why they prefer the iterative version. The idea is to go through the old and new tree, as is done in the destructor, cloning all the nodes that are in the old tree, but not new.
Using this method, the implementation of the binary search tree is always in a healthy state and can be deleted by the destructor even in an incomplete state. If an exception occurs, you only need to instruct the destructor to delete the semi-finished tree. The assignment operator can be easily implemented using Copy & Swap.
Creating a binary search tree
Optimal binary search trees are incredibly effective if they are managed properly. Some rules for binary search trees:
- A parent node has at most 2 child nodes.
- The left child node is always smaller than the parent node.
- The correct child node is always greater than or equal to the parent node.
The array that will be used to build the binary search tree:
- A basic integer array of seven values that are in unsorted order.
- The first value in the array is 10, so the first step in building the tree is to create 10 root nodes, as shown here.
- With a set of root nodes, all other values will be children of this node. Referring to the rules, the first step that will be taken to add 7 to the tree is to compare it with the root node.
- If the value 7 is less than 10, it will become the left child node.
- If the value 7 is greater than or equal to 10, it will move to the right. Since it is known that 7 is less than 10, it is designated as the left child node.
- Recursively perform comparisons for each item.
- Following the same pattern, perform the same comparison with the 14 value in the array.
- Comparing the value of 14 with the root node of 10, knowing that 14 is the right child.
- Making their way through the array, come to 20.
- Start by comparing the array with 10, which is more. Thus, they move to the right and compare it with 14, it is more than 14 and has no children on the right.
- Now there is a value of 1. Following the same pattern as the other values, they are compared from 1 to 10, moving to the left and comparing with 7 and finally with 1 left child of the 7th node.
- With a value of 5, compare it with 10. Since 5 is less than 10, go to the left and compare it with 7.
- Knowing that 5 is less than 7, continue down the tree and compare 5 with 1 value.
- If 1 does not have child nodes, and 5 is more than 1, then 5 is the right child from 1 node.
- Finally, insert the value 8 into the tree.
- With 8 less than 10, move it to the left and compare it with 7, 8 is greater than 7, so move it to the right and complete the tree, which makes 8 the right child 7.
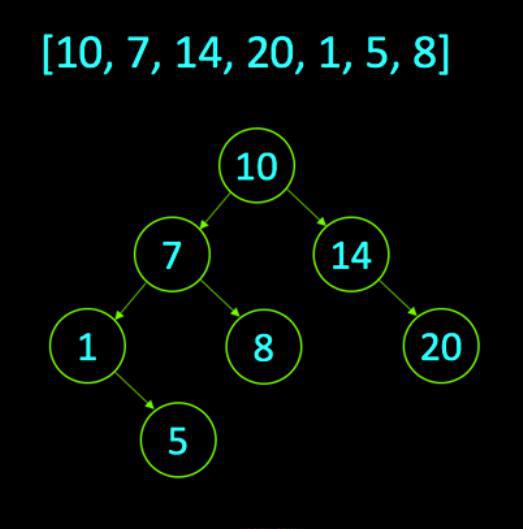
We obtain and evaluate the simple elegance of optimal binary search trees. Like many other programming topics, the strength of binary search trees depends on their ability to resolve data splitting into small related components. From now on, you can work with a complete set of data in an organized manner.
Potential Binary Search Issues
Binary search trees are good, but there are a few caveats to keep in mind. They are usually only effective if balanced. A balanced tree is a tree in which the difference between the heights of the subtrees of any node in the tree is not more than one. Consider an example that can help clarify the rules. Imagine that an array starts as sortable.
If you try to run the binary search tree algorithm in this tree, it will perform in the same way as if it were just repeating the array until the desired value is found. The power of binary search is the ability to quickly filter out unnecessary values. When a tree is not balanced, it will not give such advantages as a balanced tree.
It is very important to examine the data the user is working with when creating a binary search tree. You can integrate routines such as randomizing an array before you implement a binary search tree for integers to balance it.
Binary Search Examples
You need to determine which tree will work if 25 is inserted into the following binary search tree:
10
/ \
/ \
5 15
/ / \
/ / \
2 12 20
When x is inserted into a tree T that does not yet contain x, the key x is always placed on a new sheet. In this connection, the new tree will look like:
10
/ \
/ \
5 15
/ / \
/ / \
2 12 20
\
\
25
What tree will be obtained by inserting 7 into the next binary search tree?
10
/ \
/ \
5 15
/ / \
/ / \
2 12 20
Answer:
10
/ \
/ \
/ \
5 15
/ \ / \
/ \ / \
2 7 12 20
The binary search tree can be used to store any objects. The advantage of using a binary search tree instead of a linked list is that if the tree is reasonably balanced and looks more like a "full" tree than a "linear" one, insert, search, and all delete operations can be implemented to run in O (log N) time.