Geometry is beautiful in that, unlike algebra, where it is not always clear what and why you think, it gives an object's visibility. This wonderful world of various bodies is decorated with regular polyhedrons.
General information on regular polyhedra
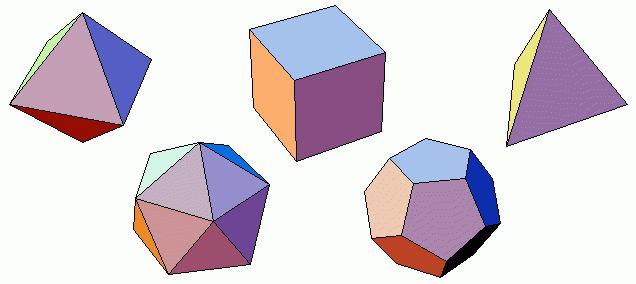
According to many, regular polyhedra, or as they are also called Platonic solids, have unique properties. Several scientific hypotheses are associated with these objects. When you start to study these geometric bodies, you understand that you know practically nothing about such a concept as regular polyhedrons. The presentation of these objects at school is not always interesting, so many do not even remember what they are called. In the memory of most people, only a cube remains. Not a single body in geometry possesses such perfection as regular polyhedrons. All the names of these geometric bodies came from ancient Greece. They mean the number of faces: the tetrahedron is tetrahedral, the hexahedron is hexagonal, the octahedron is octagonal, the dodecahedron is twelve-sided, and the icosahedron is twenty-sided. All these geometric bodies occupied the most important place in Plato's concept of the universe. Four of them represented elements or entities: a tetrahedron - fire, an icosahedron - water, a cube - earth, an octahedron - air. The dodecahedron embodied everything. He was considered the main, because he was a symbol of the universe.
A generalization of the concept of a polyhedron
A polyhedron is a collection of a finite number of polygons such that:
- each side of any of the polygons is at the same time the side of only one other polygon on the same side;
- from each of the polygons you can get to the other by moving along the adjacent polygons.
The polygons that make up the polyhedron are its faces, and their sides are edges. The vertices of the polyhedra are the vertices of the polygons. If the concept of a polygon is understood as flat closed polygons, then we come to the same definition of a polyhedron. In the case when this concept means a part of a plane that is limited by broken lines, then we should understand the surface consisting of polygonal pieces. A convex polyhedron is a body lying on one side of a plane adjacent to its face.
Another definition of a polyhedron and its elements
A polyhedron is a surface consisting of polygons that bounds a geometric body. They are:
- non-convex;
- convex (right and wrong).
A regular polyhedron is a convex polyhedron with maximum symmetry. Elements of regular polyhedrons:
- tetrahedron: 6 edges, 4 faces, 5 vertices;
- hexahedron (cube): 12, 6, 8;
- dodecahedron: 30, 12, 20;
- octahedron: 12, 8, 6;
- icosahedron: 30, 20, 12.
Euler's theorem
It establishes a connection between the number of edges, vertices, and faces that are topologically equivalent to a sphere. Adding the number of vertices and faces (B + D) of various regular polyhedra and comparing them with the number of edges, one regularity can be established: the sum of the number of faces and vertices is equal to the number of edges (P) increased by 2. A simple formula can be derived:
This formula is true for all convex polyhedra.
Key Definitions
The concept of a regular polyhedron cannot be described in one sentence. It is more ambiguous and voluminous. For the body to be recognized as such, it is necessary that it meets a number of definitions. So, a geometric body will be a regular polyhedron under the following conditions:
- it is convex;
- the same number of edges converges at each of its vertices;
- all its faces are regular polygons, equal to each other;
- all dihedral angles of it are equal.
Properties of regular polyhedra
There are 5 different types of regular polyhedra:
- Cube (hexahedron) - it has a flat angle at the apex of 90 °. It has a 3-sided angle. The sum of the flat angles at the apex is 270 °.
- Tetrahedron - flat angle at the apex - 60 °. It has a 3-sided angle. The sum of the flat angles at the top is 180 °.
- The octahedron is a flat angle at the apex - 60 °. It has a 4-sided angle. The sum of the flat angles at the top is 240 °.
- Dodecahedron - a flat angle at the apex of 108 °. It has a 3-sided angle. The sum of the flat angles at the top is 324 °.
- Icosahedron - it has a flat angle at the apex - 60 °. It has a 5-sided angle. The sum of the flat angles at the apex is 300 °.
Area of regular polyhedrons
The surface area of these geometric bodies (S) is calculated as the area of a regular polygon multiplied by the number of its faces (G):
- S = (a: 2) x 2G ctg π / p.
Volume of a regular polyhedron
This value is calculated by multiplying the volume of the regular pyramid, at the base of which is the regular polygon, by the number of faces, and its height is the radius of the inscribed sphere (r):
Volumes of regular polyhedra
Like any other geometric body, regular polyhedra have different volumes. Below are the formulas by which they can be calculated:
- tetrahedron: α x 3√2: 12;
- octahedron: α x 3√2: 3;
- icosahedron; α x 3;
- hexahedron (cube): 5 x α x 3 x (3 + √5): 12;
- dodecahedron: α x 3 (15 + 7√5): 4.
Elements of regular polyhedra
The hexahedron and octahedron are dual geometric bodies. In other words, they can turn out from each other if the center of gravity of the face of one is taken as the top of the other, and vice versa. The icosahedron and dodecahedron are also dual. Only the tetrahedron is dual to itself. By the Euclidean method, one can get a dodecahedron from a hexahedron by constructing "roofs" on the faces of a cube. The vertices of the tetrahedron will be any 4 vertices of the cube that are not adjacent in pairs along the edge. From the hexahedron (cube), you can get other regular polyhedra. Despite the fact that there are countless
regular polygons, there are only 5 regular polyhedra.
Radii of Regular Polygons
Three concentric spheres are associated with each of these geometric bodies:
- described passing through its peaks;
- inscribed, touching each of its faces in the center of it;
- median, touching all the ribs in the middle.
The radius of the sphere described is calculated by the following formula:
- R = a: 2 x tg π / g x tg θ: 2.
The radius of the inscribed sphere is calculated by the formula:
- R = a: 2 x ctg π / p x tg θ: 2,
where θ is the dihedral angle that is between adjacent faces.
The radius of the median sphere can be calculated by the following formula:
- ρ = a cos π / p: 2 sin π / h,
where h value = 4.6, 6.10 or 10. The ratio of the described and inscribed radii is symmetrical with respect to p and q. It is calculated by the formula:
- R / r = tg π / p x tg π / q.
Symmetry of Polyhedrons
The symmetry of regular polyhedra is of primary interest in these geometric bodies. By it is meant such a motion of a body in space that leaves the same number of vertices, faces and edges. In other words, under the symmetry transformation, an edge, vertex, face either retains its original position, or moves to the original position of another edge, another vertex, or face.
Symmetry elements of regular polyhedra are characteristic of all types of such geometric bodies. Here we are talking about the identity transformation, which leaves any of the points in the original position. So, when you rotate a polygonal prism, you can get several symmetries. Any of them can be represented as a product of reflections. Symmetry, which is the product of an even number of reflections, is called the line. If it is a product of an odd number of reflections, then it is called the inverse. Thus, all rotations around a straight line represent direct symmetry. Any reflection of a polyhedron is inverse symmetry.
To better understand the symmetry elements of regular polyhedra, you can take the example of a tetrahedron. Any straight line that will pass through one of the vertices and the center of this geometric figure will also pass through the center of the face opposite to it. Each of the rotations of 120 and 240 ° around the line belongs to the plural symmetries of the tetrahedron. Since it has 4 vertices and faces, we get only eight direct symmetries. Any of the lines passing through the middle of the rib and the center of this body passes through the middle of its opposite rib. Any 180 ° rotation, called a half-turn, around a straight line is symmetry. Since the tetrahedron has three pairs of edges, we get three more direct symmetries. Based on the foregoing, we can conclude that the total number of direct symmetries, including the identical transformation, will reach twelve. The tetrahedron does not have other direct symmetries, but it has 12 inverse symmetries. Therefore, the tetrahedron is characterized by only 24 symmetries. For clarity, you can build a model of a regular cardboard tetrahedron and make sure that this geometric body really has only 24 symmetries.
The dodecahedron and icosahedron are the closest to the body sphere. The icosahedron has the largest number of faces, the largest dihedral angle, and can densely cling to the inscribed sphere. The dodecahedron has the smallest angular defect, the largest solid angle at the apex. He can fill his described sphere as much as possible.
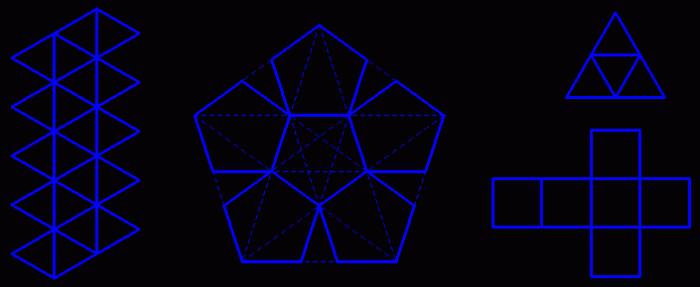
Polyhedra Sweep
The correct development polyhedra, which we all stuck together in childhood, have many concepts. If there is a set of polygons, each side of which is identified with only one side of the polyhedron, then the identification of the sides must meet two conditions:
- each polygon can be crossed over polygons having an identified side;
- identified sides must be the same length.
It is the set of polygons that satisfy these conditions that is called the polyhedron unfolding. Each of these bodies has several of them. So, for example, the cube has 11 pieces.