One of the most interesting topics in geometry from the school course is the Quadrangles (Grade 8). What types of such figures exist, what special properties do they possess? What is the uniqueness of quadrangles with angles of ninety degrees? Let's figure it all out.
What geometric shape is called a quadrilateral?
Polygons, which consist of four sides and, accordingly, of four vertices (angles), are called quadrangles in Euclidean geometry.
An interesting story is the name of this type of figure. In the Russian language, the noun “quadrangle” is formed from the phrase “four corners” (just like a “triangle” - three angles, a “pentagon” - five angles, etc.).
However, in Latin (through the mediation of which many geometric terms have come to most languages of the world) it is called quadrilateral. This word is formed from the numeral quadri (four) and the noun latus (side). So we can conclude that among the ancients this polygon was referred to only as the “four-sided”.
By the way, such a name (with emphasis on the presence of four sides in the figures of this kind, and not corners) has been preserved in some modern languages. For example, in English - quadrilateral and in French - quadrilatère.
Moreover, in most Slavic languages, the type of figures in question is still identified by the number of angles, and not by the sides. For example, in Slovak (štvoruholník), in Bulgarian (“chetirigulnik”), in Belarusian (“chatyrokhkutnik”), in Ukrainian (“chetirikutnik”), in Czech (čtyřúhelník), but in Polish the quadrilateral is called by the number of sides - czzzz.
What types of quadrangles are studied in the school curriculum
In modern geometry, 4 types of polygons with four sides are distinguished.
However, due to the too complex properties of some of them, only two types of schoolchildren are introduced to geometry lessons in school classes.
- Parallelogram (parallelogram). Opposite sides of a quadrangle of such a pair are parallel to each other and, accordingly, are also equal in pairs.
- Trapezium (trapezium or trapezoid). This quadrangle consists of two opposite sides parallel to each other. However, the other pair of parties does not have such a feature.
Types of quadrangles not studied in the school course of geometry
In addition to the above, there are two more types of quadrangles that schoolchildren are not familiar with in geometry classes, because of their special complexity.
- Deltoid (kite) - a figure in which each of the two pairs of adjacent sides is equal in length to each other. This quadrangle got its name due to the fact that in appearance it pretty much resembles the letter of the Greek alphabet - "delta".
- Antiparallelogram (antiparallelogram) - this figure is as complex as its name. In it, two opposite sides are equal, but at the same time they are not parallel to each other. In addition, the long opposite sides of this quadrangle intersect, as are the extensions of the other two, shorter sides.
Types of parallelogram
Having dealt with the main types of quadrangles, it is worth paying attention to its subspecies. So, all parallelograms, in turn, are also divided into four groups.
- Classic parallelogram.
- Rhombus (rhombus) - a quadrangular figure with equal sides. Its diagonals intersect at right angles, dividing the rhombus into four equal right triangles.
- Rectangle This name speaks for itself. Since it is a quadrangle with right angles (each of them is equal to ninety degrees). Opposite sides of it are not only parallel to each other, but also equal.
- Square Like a rectangle, it is a quadrangle with right angles, but it has all sides equal. This figure is close to a rhombus. So it can be argued that a square is a cross between a rhombus and a rectangle.
Rectangle Special Features
Considering the figures in which each of the angles between the sides is ninety degrees, it is worthwhile to pay more attention to the rectangle. So, what special features does it have that distinguish it from other parallelograms?
In order to assert that the parallelogram under consideration is a rectangle, its diagonals must be equal to each other, and each of the angles must be straight. In addition, the square of its diagonals should correspond to the sum of the squares of two adjacent sides of this figure. In other words, the classical rectangle consists of two right-angled triangles, and in them, as you know, the sum of the squares of the legs is equal to the square of the hypotenuse. The role of the hypotenuse is the diagonal of the quadrilateral under consideration.
The last of the listed features of this figure is also its special property. In addition, there are others. For example, the fact that all sides of the studied quadrangle with right angles is at the same time its height.
In addition, if you draw a circle around any rectangle, its diameter will be equal to the diagonal of the inscribed figure.
Among the other properties of this quadrangle is that it is flat and does not exist in non-Euclidean geometry. This is due to the fact that in such a system there are no quadrangular figures, the sum of the angles of which is three hundred and sixty degrees.
The square and its features
Having dealt with the signs and properties of a rectangle, it is worth paying attention to the second quadrangle with right angles known to science (this is a square).
Being in fact the same rectangle, but with equal sides, this figure has all its properties. But unlike him, a square is present in non-Euclidean geometry.
In addition, this figure has its own other distinctive features. For example, the fact that the diagonals of a square are not only equal to each other, but also intersect at right angles. Thus, like a rhombus, a square consists of four rectangular triangles into which diagonals divide it.
In addition, this figure is the most symmetrical among all the quadrangles.
What is the sum of the angles of a quadrangle
Considering the features of quadrangles of Euclidean geometry, it is worth paying attention to their angles.
So, in each of the above figures, regardless of whether it has right angles or not, their total amount is always the same - three hundred and sixty degrees. This is a unique distinguishing feature of this kind of figures.
The perimeter of the quadrangles
Having figured out what the sum of the angles of a quadrangle and other special properties of figures of this type are equal to, it is worth knowing which formulas are best used to calculate their perimeter and area.
To determine the perimeter of any quadrangle, you only need to add together the length of all its sides.
For example, in the KLMN figure, its perimeter can be calculated by the formula: P = KL + LM + MN + KN. If you substitute the numbers here, it turns out: 6 + 8 + 6 + 8 = 28 (cm).
In the case when the figure in question is a rhombus or a square, to find the perimeter, you can simplify the formula by simply multiplying the length of one of its sides by four: P = KL x 4. For example: 6 x 4 = 24 (cm).
Square quadrangle formulas
Having figured out how to find the perimeter of any figure with four corners and sides, it is worth considering the most popular and simple ways to find its area.
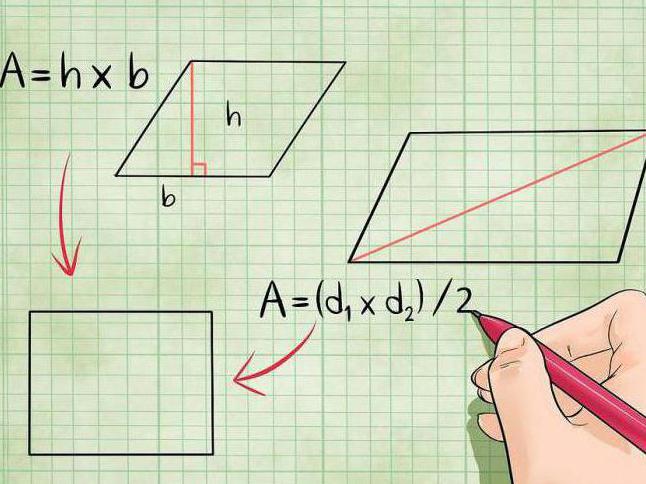
- The classic way to calculate it is to use the formula S = 1/2 KM x LN x SIN LON. It turns out that the area of any quadrangle is equal to half the product of its diagonals by the sine of the angle located between them.
- If the figure whose area you want to find is a rectangle or square (whose diagonals are always equal), you can simplify the formula by squaring the length of one diagonal and multiplying it by the sine of the angle between them and dividing everything in half. For example: S = 1/2 KM 2 x SIN LON.
- Also, when finding the area of the rectangle, information about the perimeter of the figure in question and the length of one of its sides can help. In this case, it will be most appropriate to use the formula S = KN x (P - 2 KN) / 2.
- In the case of a square, its properties allow you to use several additional formulas to find the area. For example, knowing the perimeter of a figure, you can use this option: S = P 2 / 16. And if the radius of the circle inscribed in the quadrangle is known, the square area is found in a very similar way: S = 4r 2 . If the radius of the circumscribed circle is known, then another formula is suitable: S = 2R 2 . Also, the area of the square is equal to 0.8 of the length of the line drawn from the corner of the figure to the middle of the opposite side.
- In addition to all of the above, there is also a separate formula for finding the area, designed specifically for parallelograms. It can be used, if known, the length of the two heights of the figure and the size of the angle between them. Then heights must be multiplied between themselves and the sine of the angle between them. It is worth noting that you can use this formula for all figures that relate to parallelograms (that is, to a rectangle, rhombus and square).
Other properties of quadrangles: inscribed and circled circles
Having considered the features and properties of a quadrangle as a figure of Euclidean geometry, it is worth paying attention to the ability to describe circles or to enter circles inside it:
- If the sums of the opposing corners of the figure are one hundred eighty degrees and are equal in pairs, then a circle can be freely described around such a quadrilateral.
- According to Ptolemy’s theorem, if a circle is described outside a polygon with four sides, then the product of its diagonals is equal to the sum of the products of the opposite sides of the given figure. Thus, the formula will look like this: KM x LN = KL x MN + LM x KN.
- If you build a quadrangle in which the sums of the opposite sides are equal to each other, then you can enter a circle into it.
Having figured out what a quadrangle is, what kind of quadrangle exists, which of them have only right angles between the sides and what properties they possess, it is worth remembering all this material. In particular, the formulas for finding the perimeter and area of the considered polygons. After all, figures of this form are one of the most common, and this knowledge can be useful for calculations in real life.