Judging by the popularity of the query "Fermat's theorem is a short proof", this mathematical problem really interests many. This theorem was first stated by Pierre de Fermat in 1637 on the edge of a copy of Arithmetic, where he claimed that he had her solution, it was too large to fit on the edge.
The first successful proof was published in 1995 - it was a complete proof of Fermat's theorem by Andrew Wiles. It was described as “overwhelming progress,” and led Wiles to receive the Abel Prize in 2016. Being described relatively briefly, the proof of Fermat’s theorem also proved a large part of the modularity theorem and opened up new approaches to numerous other problems and effective methods for raising modularity. These achievements advanced mathematics 100 years in advance. The proof of Fermat’s little theorem today is not out of the ordinary.

An unresolved problem stimulated the development of algebraic number theory in the 19th century and the search for proof of the modularity theorem in the 20th century. This is one of the most notable theorems in the history of mathematics and until the complete proof of Fermat's great theorem by the division method, it was in the Guinness Book of Records as the “most difficult mathematical problem”, one of the features of which is that it has the greatest number of unsuccessful proofs.
History reference
The Pythagorean equation x 2 + y 2 = z 2 has an infinite number of positive integer solutions for x, y, and z. These decisions are known as the Trinity of Pythagoras. Around 1637, Fermat wrote at the edge of the book that the more general equation a n + b n = c n has no solutions in natural numbers if n is an integer greater than 2. Although Fermat himself claimed to have a solution to his problem, he left no details about her evidence. The elementary proof of Fermat's theorem, stated by its creator, was rather his boastful invention. The book of the great French mathematician was discovered 30 years after his death. This equation, called Fermat's Last Theorem, remained unresolved in mathematics for three and a half centuries.
The theorem eventually became one of the most noticeable unresolved problems in mathematics. Attempts to prove this caused a significant development of number theory, and over time, Fermat's last theorem became known as an unsolved problem in mathematics.
A Brief History of Evidence
If n = 4, as proved by Fermat himself, it suffices to prove the theorem for indices n, which are primes. Over the next two centuries (1637–1839), the hypothesis was proved only for primes 3, 5, and 7, although Sophie Germain updated and proved an approach that was relevant to the entire class of primes. In the mid-19th century, Ernst Kummer extended this and proved the theorem for all regular primes, as a result of which irregular primes were analyzed individually. Based on Kummer's work and using sophisticated computer research, other mathematicians were able to expand the solution of the theorem, with the goal of covering all the main indicators up to four million, but the evidence for all exhibitors was still inaccessible (this means that mathematicians usually considered the solution to the theorem impossible, extremely complex, or unattainable with modern knowledge).
The work of Shimura and Taniyama
In 1955, Japanese mathematicians Goro Shimura and Yutaka Taniyama suspected that there was a connection between elliptic curves and modular forms, two completely different areas of mathematics. Known at that time as the Taniyam-Shimur-Weil hypothesis and (ultimately) as the modularity theorem, it existed on its own, with no apparent connection with Fermat's last theorem. It itself was widely regarded as an important mathematical theorem, but at the same time it was considered (like Fermat's theorem) impossible to prove. At the same time, the proof of Fermat's great theorem (by the method of division and application of complex mathematical formulas) was carried out only half a century later.
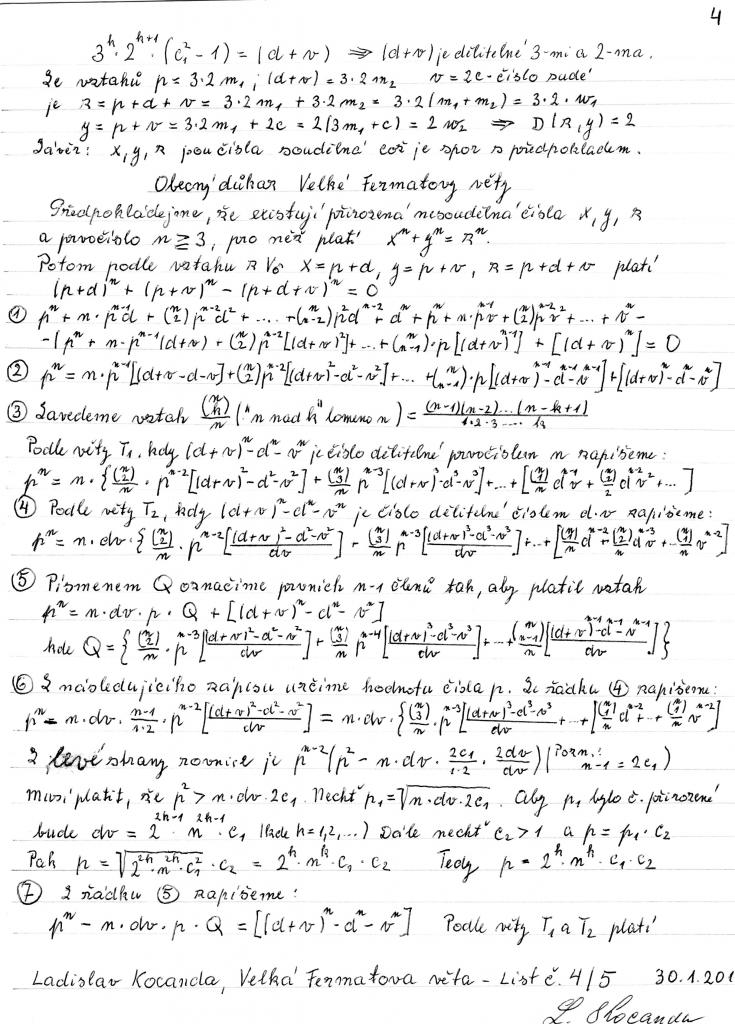
In 1984, Gerhard Frey noticed an obvious connection between the two previously unrelated and unresolved issues. Full confirmation that the two theorems were closely related was published in 1986 by Ken Ribet, which was based on a partial proof of Jean-Pierre Serre, who proved all but one part, known as the “epsilon hypothesis”. Simply put, these works of Frey, Serra and Ribe showed that if the modularity theorem could be proved, at least for a semistable class of elliptic curves, then the proof of Fermat’s last theorem will also be open sooner or later. Any solution that may contradict Fermat’s last theorem can also be used to contradict the modularity theorem. Therefore, if the modularity theorem turned out to be true, then by definition there cannot be a solution that contradicts Fermat's last theorem, which means that it should soon be proved.
Although both theorems were complex problems for mathematics, considered unsolvable, the work of two Japanese was the first assumption about how Fermat's last theorem could be continued and proved for all numbers, and not just for some. Important for researchers who chose the research topic was the fact that, unlike Fermat’s last theorem, the modularity theorem was the main active area of research for which proof was developed, and not just historical strangeness, so the time spent on its work could be justified from a professional point of view. However, the general opinion was that the solution of the Taniyama-Shimura hypothesis was not practical.
Fermat's Great Theorem: Wiles Proof
Upon learning that Ribet proved Frey's theory correct, the English mathematician Andrew Wiles, who was interested in Fermat's last theorem from his childhood and has experience with elliptic curves and related domains, decided to try to prove the Taniyama-Shimura hypothesis as a way to prove Fermat's last theorem. In 1993, six years after announcing his goal, secretly working on the problem of solving the theorem, Wiles was able to prove a related hypothesis, which, in turn, would help him prove Fermat's last theorem. Wiles' document was huge in size and scale.
The flaw was discovered in one part of his original article during the review and required another year of collaboration with Richard Taylor to jointly solve the theorem. As a result, Wiles' final proof of Fermat’s great theorem was not long in coming. In 1995, it was published on a much smaller scale than Wiles' previous mathematical work, demonstrating clearly that he was not mistaken in his previous conclusions about the possibility of proving the theorem. Wiles' achievement was widely disseminated in the popular press and popularized in books and television programs. The remaining parts of the Taniyama-Shimur-Weil hypothesis, which were now proved and known as the modularity theorem, were subsequently proved by other mathematicians who were based on the work of Wiles between 1996 and 2001. For his achievement, Wiles was honored and received numerous awards, including the 2016 Abel Prize.

Wiles' proof of Fermat's last theorem is a special case of the solution of the modularity theorem for elliptic curves. Nevertheless, this is the most famous case of such a large-scale mathematical operation. Together with the solution of the Ribet theorem, the British mathematician also obtained a proof of Fermat's last theorem. Fermat's last theorem and modularity theorem were almost universally considered unprovable by modern mathematicians, but Andrew Wiles was able to prove to the whole scientific world that even pundits are capable of being mistaken.
Wiles first announced his discovery on Wednesday, June 23, 1993, at a lecture in Cambridge entitled "Modular Forms, Elliptic Curves, and Galois Representations." However, in September 1993 it was found that his calculations contained an error. A year later, on September 19, 1994, in what he would call “the most important moment of his working life”, Wiles came across a revelation that allowed him to correct the solution of the problem to a level where it could satisfy the mathematical community.
Work characteristic
Proof of Fermat's theorem Andrew Wiles uses many methods from algebraic geometry and number theory and has many branches in these areas of mathematics. He also uses standard constructions of modern algebraic geometry, such as the category of schemes and the Iwasawa theory, as well as other methods of the 20th century that were not available to Pierre Fermat.
Two articles containing evidence comprise 129 pages that have been written over seven years. John Coates described this discovery as one of the greatest achievements of number theory, and John Conway called it the main mathematical achievement of the 20th century. Wiles, in order to prove Fermat's last theorem by proving the modularity theorem for the particular case of semistable elliptic curves, developed effective methods for raising modularity and opened up new approaches to numerous other problems. For the solution of Fermat's last theorem, he was knighted and received other awards. When it became known that Wiles won the Abel Prize, the Norwegian Academy of Sciences described his achievement as "a delightful and elementary proof of Fermat's last theorem."
How it was
One of the people who analyzed Wiles' original manuscript with a solution to the theorem was Nick Katz. During his review, he asked the Briton a number of clarifying questions that made Wiles admit that his work clearly contained a gap. In one critical part of the proof, a mistake was made that gave an estimate for the order of a particular group: the Euler system used to extend the Kolyvagin and Flach method was incomplete. The mistake, however, did not make his work useless - every part of Wiles' work was very significant and innovative in itself, like many of the developments and methods that he created in the course of his work and which affected only one part of the manuscript. However, in this original paper, published in 1993, there really was no proof of Fermat's great theorem.

Wiles spent almost a year trying to find a solution to the theorem again - first alone, and then in collaboration with his former student Richard Taylor, but everything seemed to be futile. By the end of 1993, rumors circulated that Wiles' evidence had failed in the verification, but how serious this failure was was not known. Mathematicians began to put pressure on Wiles to reveal the details of his work, regardless of whether it was completed or not, so that a wider community of mathematicians could research and use everything that he managed to achieve. Instead of quickly correcting his mistake, Wiles only discovered additional complex aspects in the proof of Fermat's great theorem, and finally realized how complicated it is.
Wiles states that on the morning of September 19, 1994, he was on the verge of quitting and surrendering, and almost came to terms with the fact that he had failed. He was ready to publish his unfinished work, so that others could build on it and find what he was wrong about. The English mathematician decided to give himself one last chance and analyzed the theorem for the last time in order to try to understand the main reasons why his approach did not work, when he suddenly realized that the Kolyvagin-Flack approach would not work until he connected the proof to the process Iwasawa's theory, making it work.
On October 6, Wiles asked three colleagues (including Faltins) to consider his new work, and on October 24, 1994, he presented two manuscripts - “Modular elliptic curves and Fermat's last theorem” and “Theoretical properties of the ring of some Hecke algebras”, the second of which is Wiles He wrote together with Taylor and proved that certain conditions were met that were necessary to justify the corrected step in the main article.
These two articles were checked and finally published as a full-text edition in the journal "Annals of Mathematics" for May 1995. Andrew’s new calculations were widely analyzed and the scientific community eventually recognized them. In these papers, the modularity theorem for semistable elliptic curves was established - the last step in proving Fermat's great theorem, 358 years after it was created.
History of the great problem
The solution to this theorem was considered the biggest problem in mathematics for many centuries. In 1816 and 1850, the French Academy of Sciences offered a prize for a general proof of Fermat's great theorem. In 1857, the Academy awarded 3,000 francs and a gold medal to Kummer for research on ideal numbers, although he did not apply for the prize. Another prize was offered to him in 1883 by the Brussels Academy.
Wolfskel Prize
In 1908, the German industrialist and amateur mathematician Paul Wolfskel bequeathed 100,000 gold marks (a large sum for that time) to the Göttingen Academy of Sciences so that this money would become a prize for complete proof of Fermat's great theorem. On June 27, 1908, the Academy published nine award rules. Among other things, these rules required the publication of evidence in a peer-reviewed journal. The prize was to be awarded only two years after publication. The deadline for the competition was to expire on September 13, 2007 - about a century after its inception. On June 27, 1997, Wiles received Wolfshel prize money, and then another $ 50,000. In March 2016, he received 600,000 euros from the Norwegian government as part of the Abel Prize for “stunning proof of Fermat’s last theorem using the modularity hypothesis for semistable elliptic curves, opening a new era in number theory.” It was a world triumph of the humble Englishman.

Prior to Wiles' proof, Fermat's theorem, as mentioned earlier, was considered completely unsolvable for centuries. Thousands of incorrect evidence at various times was submitted to the Wolfskel committee, amounting to approximately 10 feet (3 meters) of correspondence. Only in the first year of the existence of the prize (1907-1908), 621 applications were submitted with a claim to the solution of the theorem, although by the 1970s their number had decreased to about 3-4 applications per month. According to F. Schlichting, a Wolfschel reviewer, most of the evidence was based on elementary methods taught in schools and was often presented as “people with a technical background, but an unsuccessful career”. According to mathematician historian Howard Aves, Fermat’s last theorem set a record — a theorem with the most false evidence.
Farm laurels went to the Japanese
As mentioned earlier, around 1955, the Japanese mathematicians Goro Shimura and Yutaka Taniyama discovered a possible connection between two apparently different branches of mathematics - elliptic curves and modular forms. The modularity theorem obtained as a result of their research (at that time known as the Taniyama-Shimura hypothesis) states that each elliptic curve is modular, which means that it can be associated with a unique modular form.
The theory was initially rejected as unlikely or highly speculative, but was taken more seriously when number theorist Andre Weil found evidence to support Japanese conclusions. As a result, the hypothesis was often called the Taniyama-Shimura-Weil hypothesis. It has become part of the Langlands program, which is a list of important hypotheses that require proof in the future.
Even after serious attention, the hypothesis has been recognized by modern mathematicians as extremely difficult or possibly inaccessible to prove. Now it is this theorem that is waiting for its Andrew Wiles, who could surprise the whole world with its solution.
Fermat's theorem: Perelman's proof
, , , . , , .