Answering the question of what is called acceleration in physics, it should be said that this is a vector quantity that shows how the speed changes per unit time. In Newtonian vector mechanics, acceleration is usually denoted by a → and measured in the system of international units in m / s 2 .
What is called acceleration?
According to the postulates of Newtonian mechanics, a particle (body) cannot move along a curved trajectory if no external forces act on it, that is, such a particle will move linearly. At the same time, a particle moving along a direct trajectory can increase its speed or decrease it if the vector of the force acting on it is parallel to its velocity vector.
In classical mechanics, the answer to what is called acceleration is the change in speed over a given period of time, that is, a = dv / dt, which is mathematically interpreted as the derivative of speed with respect to time.
Acceleration and Newton's Second Law
The acceleration of a body of mass m, in accordance with Newton’s second law, is proportional to the resulting F force that acts on this body, that is, F = ma. This expression is valid for any inertial reference frame, that is, such a system that is at rest, or moves linearly and uniformly.
We give the following examples of using this formula for finding acceleration or force acting on a body.
- Acceleration during free fall on our planet owes its existence to the force of gravity acting on all objects without exception, which have some non-zero mass. It is denoted by g and is equal to 9.8 m / s 2 near the surface of the earth. This means that if any body in the gravitational field of the Earth is in a state of free fall, then it will increase its speed for every second of the flight by 9.8 m / s. After the start of such a fall, the velocity at each moment of time for the body is determined by the formula: v = at = gt = 9.8t. In this case, the force of gravity acting on this body is equal to F = mg. Note that, in reality, in a free fall , air resistance also acts on the body, a force that depends on speed, and at a certain value it becomes equal in magnitude to gravity. In this case, the body moves at a constant speed.
- Another example when you can use Newton’s second law is the process of braking or accelerating a car.
Medium and Instant Acceleration
When a body moves, then the velocity vector and its module in the general case change with time, but the velocity vector is always directed to the trajectory along the tangent. For example, let at t 1 moment in time the body move with v 1 → speed, and at t 2 point in time with speed v 2 → . Answering the question of what is called average acceleration, we say that this physical quantity is determined by the formula: a → = Δv → / Δt, in which Δt = t 2 - t 1 and Δv → = v 2 → -v 1 → . Note that the acceleration vector is directed in the same way as the velocity change vector Δv → .
Instantaneous acceleration in physics is defined as the time derivative of the velocity for a particular moment in time, that is, a → = dv → / dt. Given that the velocity is a time derivative of the body coordinate, one can obtain acceleration if we take the time derivative from the body coordinate a second time, that is, a = d 2 r / dt 2 , where r is the body coordinate at t moment in time.
Circular uniform motion
Uniform and circular is such a movement, a body or a particle in which it moves around the circumference of a certain constant radius R with a constant velocity modulus V, that is, this body or particle travels the same path for the same time intervals. Since the body moves along the trajectory of a circle, it constantly changes the direction of speed.
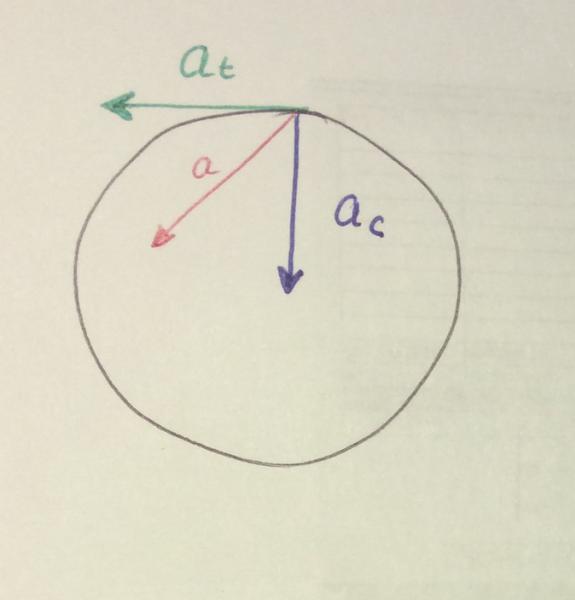
If the acceleration vector is decomposed into a pair of components so that one of them is directed to the trajectory of motion along the tangent, and the second to the center of the circle along the radius R, then the first component is called tangential, and the second is normal. Given that the motion is uniform, the tangential component of the acceleration is zero, and the normal component is a constant, which is the answer to the question of what is called centripetal acceleration. This acceleration is aimed at changing the trajectory of the object and does not change the speed itself. Centripetal acceleration in physics is calculated by the formula a = v 2 / R.
Rectilinear, uniformly accelerated movement
If we consider the rectilinear motion of the body, that is, with this motion, the velocity vector does not change its direction, but only its modulus changes, then the formula at any time t for time can be written as follows: v = v0 + ∫ t 0 a (t) dt, where v 0 is the initial nonzero velocity. In this expression, there is a dependence of acceleration on time. If the force acting on the body is constant, then the acceleration will not change over time, in this case we get a simple expression at t moment of time for speed: v = v 0 + at.
The integral expression for speed can be integrated again, then we get an expression for the path that this body travels in time t. Given that the acceleration is constant, we obtain the formula: x - x 0 = v 0 t + at 2/2, in which x - x 0 is the difference between the final and initial coordinates of the body, which shows the path traveled by it.