Geometry is not only a subject in a school for which you need to get an excellent grade. It is also the knowledge that is often required in life. For example, when building a house with a high roof, you need to calculate the thickness of the logs and their number. This is easy if you know how to find height in an isosceles triangle. Architectural structures are based on knowledge of the properties of geometric shapes. Forms of buildings often visually resemble them. Egyptian pyramids, packages of milk, artistic embroidery, northern paintings and even pies - these are all triangles surrounding a person. As Plato said, the whole world is based on triangles.
Isosceles triangle
To make it clearer what will be discussed further, it is worth recalling the basics of geometry a little.
A triangle is isosceles if it has two equal sides. They are always called lateral. The party, the sizes of which differ, is called the base.
Basic concepts
Like any science, geometry has its own basic rules and concepts. There are a lot of them. Consider only those without which our topic will be somewhat incomprehensible.
Height is a straight line drawn perpendicular to the opposite side.
A median is a segment directed from any vertex of a triangle exclusively to the middle of the opposite side.
The angle bisector is a beam that divides the angle in half.
The bisector of a triangle is a straight line, or rather, a segment of the bisector of the angle connecting the vertex to the opposite side.
It is very important to remember that the angle bisector is necessarily a ray, and the triangle bisector is part of such a ray.
Base angles
The theorem says that the angles located at the base of any isosceles triangle are always equal. To prove this theorem is very simple. Consider the depicted isosceles triangle ABC, in which AB = BC. From the corner of the ABC, it is necessary to draw a bisector of the VD. Now, two resulting triangles should be considered. By the condition AB = BC, the side of the VD for the triangles is common, and the angles of the AED and SVD are equal, because the VD is a bisector. Remembering the first sign of equality, we can safely conclude that the triangles under consideration are equal. Therefore, all the corresponding angles are equal. And, of course, the parties, but by now we will return later.
The height of the isosceles triangle
The main theorem on which the solution of almost all problems is based is as follows: the height in an isosceles triangle is a bisector and a median. To understand its practical meaning (or essence), an auxiliary manual should be made. To do this, cut an isosceles triangle from paper. The easiest way to do this is from a regular notebook sheet in a box.
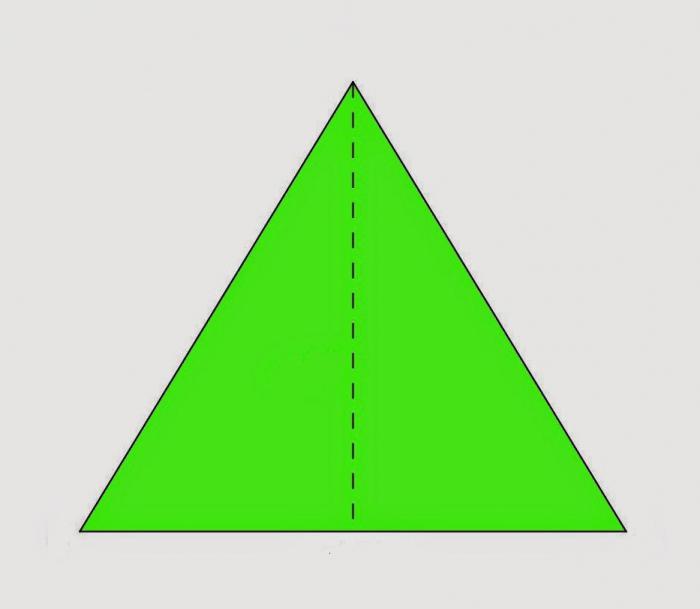
Bend the resulting triangle in half, aligning the sides. What happened? Two equal triangles. Now you should check the guesswork. Expand the resulting origami. Draw a fold line. Using a protractor, check the angle between the drawn line and the base of the triangle. What does the angle of 90 degrees mean? The fact that the drawn line is perpendicular. By definition, height. How to find the height in an isosceles triangle, we figured out. Now let's take care of the corners at the top. Using the same protractor, check the angles formed now already tall. They are equal. So, the height is also a bisector. Armed with a ruler, measure the segments into which the base breaks the height. They are equal. Therefore, the height in the isosceles triangle divides the base in half and is the median.
Proof of the theorem
Visual aid clearly demonstrates the truth of the theorem. But geometry is a fairly accurate science, and therefore requires proof.
During the consideration of equality of angles at the base, equality of triangles was proved. Recall that the VD is a bisector, and the triangles of the AED and the SVD are equal. The conclusion was this: the corresponding sides of the triangle and, of course, the angles are equal. Hence, AD = SD. Therefore, VD is the median. It remains to prove that the VD is height. Based on the equality of the considered triangles, it turns out that the angle of the ADV is equal to the angle of the ADD. But these two angles are adjacent, and, as you know, give a total of 180 degrees. Therefore, what are they equal to? Of course, 90 degrees. Thus, VD is the height in an isosceles triangle drawn to the base. Q.E.D.
Key features
- To successfully solve problems, you should remember the main signs of isosceles triangles. They are, as it were, the opposite of theorems.
- If the solution of the problem reveals the equality of two angles, then you are dealing with an isosceles triangle.
- If you managed to prove that the median is at the same time the height of the triangle, feel free to conclude that the triangle is isosceles.
- If the bisector is also the height, then, based on the main features, the triangle is classified as isosceles.
- And, of course, if the median also acts as a height, then such a triangle is an isosceles.
Height formula 1
However, for most tasks it is required to find the arithmetic value of the height. That is why we will consider how to find height in an isosceles triangle.
Let us return to the ABC figure presented above, in which a is the sides and c is the base. VD - the height of this triangle, it is denoted by h.
What is an AVD triangle? Since the VD is the height, the triangle of the AED is rectangular, the leg of which must be found. Using the formula of Pythagoras, we get:
AB² = AD² + VD²
Having determined from the expression VD and substituting the previously accepted notation, we obtain:
N² = a² - (w / 2) ².
It is necessary to extract the root:
= √² - ² / 4.
If we take out from under the sign of the root ¼, then the formula will look like:
H = ½ √4a² - ².
So is the height in an isosceles triangle. The formula follows from the Pythagorean theorem. Even if you forget this symbolic record, then, knowing the method of finding, you can always deduce it.
Height formula 2
The formula described above is the main one and is most often used in solving most geometric problems. But she is not the only one. Sometimes in the condition, instead of the base, the value of the angle is given. With such data, how to find the height in an isosceles triangle? To solve such problems, it is advisable to use a different formula:
H = a / sin α,
where H is the height directed to the base,
a - side
α is the angle at the base.
If the problem gives the value of the angle at the vertex, then the height in the isosceles triangle is as follows:
H = a / cos (β / 2),
where H is the height lowered to the base,
β is the angle at the apex,
and - the side.
Rectangular isosceles triangle
A triangle with a vertex of 90 degrees has a very interesting property. Consider a right triangle ABC. As in previous cases, VD is the height directed to the base.
The angles at the base are equal. To calculate them is not a big deal:
α = (180 - 90) / 2.
Thus, the angles at the base are always 45 degrees. Now consider the ADV triangle. It is also rectangular. Find the angle of the AED. By simple calculations we get 45 degrees. And, therefore, this triangle is not only rectangular, but also isosceles. Parties AD and VD are the sides and are equal to each other.
But the side of HELL at the same time is half the side of the AU. It turns out that the height in an isosceles triangle is equal to half the base, and if written in the form of a formula, we get the following expression:
H = b / 2.
It should not be forgotten that this formula is an exclusively special case, and can only be used for rectangular isosceles triangles.
Golden triangles
Very interesting is the golden triangle. In this figure, the ratio of the side to the base equals the value called the Phidias number. The angle located at the top is 36 degrees, at the base - 72 degrees. The Pythagoreans admired this triangle. The principles of the golden triangle form the basis of many immortal masterpieces. The five-pointed star known to all is built at the intersection of isosceles triangles. For many creations, Leonardo da Vinci used the principle of the "golden triangle." The composition "Gioconda" is based precisely on the figures that create a regular star pentagon.
The painting “Cubism”, one of the works of Pablo Picasso, captivates the eye with the isosceles triangles underlying it.