From everyday experience, we can confirm the following conclusion: the speed and direction of movement of the body can only change during its interaction with another body. This gives rise to the phenomenon of inertia, which we will discuss in this article.
What is inertia? Life observation example
Consider the cases when some body at the initial stage of the experiment is already in motion. Later we will see that a decrease in speed and a stop of the body cannot occur arbitrarily, because the reason for this is the action of another body on it.
You probably have seen more than once that passengers who are traveling in vehicles suddenly lean forward while braking or push themselves on their side in a sharp bend. Why? We will explain further. When, for example, athletes run a certain distance, they try to develop maximum speed. Having run through the finish line, you can no longer run, but you can’t stop abruptly, and therefore the athlete runs a few more meters, that is, makes inertia movement.
From the above examples, we can conclude that all bodies have the peculiarity of maintaining the speed and direction of motion, not being able to immediately change subsequently the actions of another body. It can be assumed that in the absence of external action, the body will retain both speed and direction of motion for as long as desired. So what is inertia? This is the phenomenon of maintaining the speed of the body in the absence of exposure to other bodies.
Discovery of inertia
Such a property of the bodies was discovered by the Italian scientist Galileo Galilei. Based on his experiments and reasoning, he argued: if the body does not interact with other bodies, then it either remains in a state of calm, or moves in a straight and uniform manner. His discoveries entered into science as the Law of Inertia, but Rene Descartes formulated it in more detail, and Isaac Newton introduced it into his system of laws.
An interesting fact: the inertia, the definition of which Galileo brought us, was considered in ancient Greece by Aristotle, but due to the insufficient development of science, an exact formulation was not given. Newton's first law states: there are such
reference systems, with respect to which a body that moves forward, keeps its speed constant, unless other bodies act on it. The inertia formula in a single and generalized form is absent, but below we give many other formulas that reveal its features.
Inertia of bodies
We all know that the speed of a person, car, train, ship or other bodies increases gradually when they begin to move. All of you saw the launch of missiles on TV or the take-off of aircraft at the airport - they increase speed not jerkily, but gradually. Observations, as well as everyday practice, indicate that all bodies have a common feature: the speed of movement of bodies in the process of their interaction changes gradually, and therefore it takes some time to change them. This feature of the bodies is called inertia.
All bodies are inert, but not all have the same inertia. Of the two interacting bodies, it will be higher for the one that will gain less acceleration. So, for example, when shot, the gun acquires less acceleration than the cartridge. With the mutual repulsion of the adult skater and the child, the adult receives less acceleration than the child. This indicates that the inertia of an adult is greater.
To characterize the inertia of the bodies, a special value was introduced — the mass of the body; In order to be able to compare the masses of different bodies, the mass of any of them must be taken into account per unit. Her choice may be arbitrary, but it should be convenient for practical use. In the SI system, a mass of a special standard made of a solid alloy of platinum and iridium was taken per unit. It bears the famous name for all of us - a kilogram. It should be noted that the inertia of a solid is of 2 types: translational and rotational. In the first case, the measure of inertia is mass, in the second - the moment of inertia, which we will talk about later.
Moment of inertia
So called a scalar physical quantity. In the SI system, the unit of measurement of the moment of inertia is kg * m 2 . The generalized formula is as follows:
Here m i is the mass of body points, r i is the distance from the points of the body to the z axis in the spatial coordinate system. In verbal interpretation, we can say this: the moment of inertia is determined by the sum of the products of elementary masses times the square of the distance to the base set.
There is another formula that characterizes the determination of the moment of inertia:
Here dm is the mass of the element, r is the distance from the element dm to the z axis. Verbally, it can be formulated as follows: the moment of inertia of a system of material points or a body relative to a pole (point) is the algebraic sum of the masses of the material points that make up the body and the square of their distance from the pole 0.
It is worth mentioning that there are 2 types of moments of inertia - axial and centrifugal. There is also such a thing as the main moments of inertia (GMI) (relative to the main axes). As a rule, they are always different from each other. Now it is possible to calculate the moments of inertia for many bodies (cylinder, disk, ball, cone, sphere, etc.), but we will not go deep into the refinement of all formulas.
Reference systems
Newton's 1st law dealt with uniform rectilinear motion, which can only be considered in a certain reference frame. Even an approximate analysis of mechanical phenomena shows that the law of inertia is far from being satisfied in all reference frames.
Consider a simple experiment: put the ball on a horizontal table in the car and observe its movement. If the train is in a state of calmness with respect to the Earth, then the ball will remain calm until we act on it with a different body (for example, hand). Therefore, in the frame of reference that is connected with the Earth, the law of inertia is fulfilled.
Imagine that a train will travel uniformly and rectilinearly relative to the Earth. Then, in the frame of reference that is connected with the train, the ball will maintain a state of calm, and in the one that is connected with the Earth, the state of uniform and rectilinear movement. Consequently, the law of inertia is satisfied not only in the frame of reference connected with the Earth, but also in all others moving uniformly and rectilinearly relative to the Earth.
Now imagine that a train is rapidly gaining speed or turning abruptly (in all cases, it moves with acceleration relative to the Earth). Then, as before, the ball retains the uniform and rectilinear movement that it had before the acceleration of the train. However, with respect to the train, the ball itself leaves the state of calm, although there are no bodies that would take it out of it. This means that in the reference frame associated with the acceleration of the train relative to the Earth, the law of inertia is violated.
So, reference frames in which the law of inertia is fulfilled are called inertial. And those in which it is not fulfilled are non-inertial. It is simple to define them: if the body moves uniformly and rectilinearly (in some cases it is calm), then the system is inertial; if the movement is uneven - non-inertial.
Inertia force
This is a rather ambiguous concept, and therefore we will try to examine it in more detail as much as possible. We give an example. You are standing quietly on the bus. Suddenly, he begins to move, which means he is gaining acceleration. You will lean back past your will. But why? Who pulled you? From the point of view of the observer on Earth (inertial reference frame), you remain in place, while the first Newton's law is fulfilled. From the point of view of the observer in the bus itself, you begin to move backward, as if under some force. In fact, your legs, which are connected by friction with the floor of the bus, went forward with him, and you,
losing balance, had to fall back. Thus, to describe the motion of a body in a non-inertial reference frame, it is necessary to introduce and take into account additional forces that act on the part of the body’s bonds with such a system. These forces are the forces of inertia.
It must be taken into account that they are fictitious, because there is not a single body or field under the influence of which you began to move in the bus. Newton’s laws do not apply to inertial forces, but their use along with “real” forces allows one to describe the motion of arbitrary non-inertial reference frames using various tools. This is the whole point of introducing inertia forces.
So, now you know what inertia is, the moment of inertia and inertial systems, the forces of inertia. We move on.
Translational motion systems
Let on a certain body located in a non-inertial reference frame, moving with acceleration a 0 relatively inertial, the force F acts. For such a non-inertial system, the analogue equation of Newton’s second law has the form:
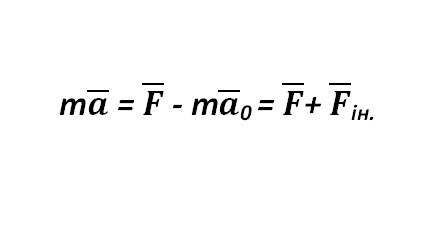
Where a 0 is the acceleration of a body with mass m , which is caused by the action of the force F relative to the non-inertial reference frame; F і - the force of inertia . The force F on the right-hand side is “real” in the sense that it is the result of the interaction of bodies, depending only on the difference in the coordinates and velocities of the interacting material points, which do not change when moving from one reference frame to another, moving progressively. Therefore, the force F does not change either. It is invariant with respect to such a transition. But F і arises not because of the interaction of bodies, but because of the accelerated motion of the reference system, because of which it changes during the transition to another accelerated system, therefore it is not invariant.
Centrifugal inertia
Consider the behavior of bodies in a non-inertial reference frame. XOY rotates relative to the inertial system, which we will consider the Earth, with a constant angular velocity ω. An example is the system in the figure below.
Above is a disk, where a radially directed rod is fixed, and also a blue ball is put on, “tied” to the disk axis with an elastic rope. Until the disc rotates, the rope does not warp. However, when the disk is untwisted, the ball gradually stretches the rope until the elastic force F cf becomes such that it is equal to the product of the mass of the ball m and its normal acceleration a p = -ω 2 R, that is, F cf = -mω 2 R , where R is the radius of the circle that describes the ball as it rotates around the system.
If the angular velocity ω of the disk remains constant, then the ball will stop moving about the axis OX. In this case, relative to the XOY reference system, which is connected to the disk, the ball will be in a state of calm. This is explained by the fact that in this system, in addition to the force F cf, the inertia force F cf acts on the ball, which is directed along the radius from the axis of rotation of the disk. The force, which has the form, as in the formula below, is called the centrifugal force of inertia. It can occur only in rotating reference frames.
Coriolis Force
It turns out that when bodies move relative to rotating reference frames, in addition to centrifugal inertia, another force acts on them - Coriolis. It is always perpendicular to the velocity vector of the body V, which means that it does not do any work on this body. We emphasize that the Coriolis force manifests itself only when the body moves relative to the non-inertial reference frame, which rotates. Her formula is as follows:
Since the expression (v * ω) is a vector product of the vectors given in parentheses, we can conclude that the direction of the Coriolis force is determined by the rule of the gimlet relative to them. Its module is equal to:
Here Ө is the angle between the vectors v and ω .
Finally
Inertia is an amazing phenomenon that haunts every person hundreds of times every day, even though we ourselves do not notice it. We think that the article gave you important answers to questions about what is inertia, what is force and moments of inertia, who discovered the phenomenon of inertia. We are sure you were interested.