How to find the minimum and maximum points of a function: features, methods and examples

The function and study of its features occupies one of the key chapters in modern mathematics. The main component of any function is graphs depicting not only its properties, but also the parameters of the derivative of this function. Let's look into this difficult topic. So, what is the best way to look for the maximum and minimum points of a function?

Function: Definition

Any variable that somehow depends on the values ​​of another quantity can be called a function. For example, the function f (x ² ) is quadratic and determines the values ​​for the whole set x. Suppose that x = 9, then the value of our function will be 9 ² = 81.

Functions can be of various types: logical, vector, logarithmic, trigonometric, numerical and others. Their study was carried out by such outstanding minds as Lacroix, Lagrange, Leibniz and Bernoulli. Their works serve as a stronghold in modern methods of studying functions. Before you find the minimum points, it is very important to understand the very meaning of the function and its derivative.

Derivative and its role

All functions are dependent on their variables, which means that they can change their value at any time. On the graph, this will be depicted as a curve, which then drops, then rises along the ordinate (this is the whole set of numbers "y" along the vertical of the graph). So the definition of the maximum and minimum points of a function is precisely connected with these “fluctuations”. Let us explain what this relationship is.

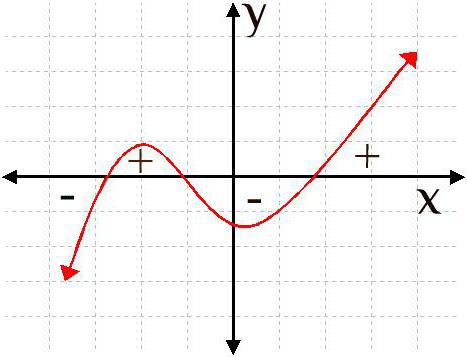
The derivative of any function is depicted on the graph in order to study its main characteristics and calculate how quickly the function changes (that is, it changes its value depending on the variable "x"). The moment the function increases, the graph of its derivative will also increase, but at any second the function may begin to decrease, and then the graph of the derivative will decrease. Those points at which the derivative passes from the minus sign to the plus are called minimum points. In order to know how to find the minimum points, you should better understand the concept of derivative.

How to calculate the derivative?

The definition and calculation of a derivative function implies several concepts from differential calculus. In general, the very definition of a derivative can be expressed as follows: this is the quantity that shows the rate of change of a function.

For many students, the mathematical method of determining it seems complicated, but in fact, everything is much simpler. It is only necessary to follow the standard plan for finding the derivative of any function. The following describes how to find the minimum point of a function without applying differentiation rules and without memorizing the table of derivatives.

1. The derivative of a function can be calculated using a graph. To do this, it is necessary to depict the function itself, then take one point on it (point A in Fig.) Draw a line vertically down to the abscissa axis (point x ₀ ), and draw a tangent to the function graph at point A. The abscissa and tangent axis form a certain angle a. To calculate the value of how quickly the function grows, it is necessary to calculate the tangent of this angle a.
2. It turns out that the tangent of the angle between the tangent and the direction of the x axis is the derivative of the function in a small area with point A. This method is considered a geometric way of determining the derivative.

Methods of function research

In the school mathematics program, it is possible to find the minimum point of a function in two ways. We have already analyzed the first method using the graph, but how to determine the numerical value of the derivative? To do this, you need to learn several formulas that describe the properties of the derivative and help to convert variables of type "x" into numbers. The following method is universal, therefore it can be applied to almost all kinds of functions (both geometric and logarithmic).

1. It is necessary to equate the function to the derivative function, and then simplify the expression using the rules of differentiation.
2. In some cases, when a function is given in which the variable "x" is in the divider, it is necessary to determine the range of acceptable values ​​by excluding the point "0" from it (for the simple reason that in mathematics it is by no means divisible by zero).
3. After that, the original form of the function should be transformed into a simple equation, equating the whole expression to zero. For example, if a function looked like this: f (x) = 2x ³ + 38x, then according to the rules of differentiation its derivative is f '(x) = 3x ² +1. Then we transform this expression into an equation of the following form: 3x ² +1 = 0.
4. After solving the equation and finding the points "x", you should depict them on the abscissa axis and determine whether the derivative in these areas between the marked points is positive or negative. After the designation, it will become clear at what point the function begins to decrease, that is, it changes sign from minus to the opposite. It is in this way that you can find both the minimum and maximum points.

Differentiation rules

The most basic component in the study of a function and its derivative is knowledge of the rules of differentiation. Only with their help can bulky expressions and large complex functions be transformed. Let's get acquainted with them, there are a lot of them, but they are all very simple due to the regular properties of both power and logarithmic functions.

1. The derivative of any constant is zero (f (x) = 0). That is, the derivative f (x) = x ⁵ + x - 160 takes the following form: f '(x) = 5x ⁴ +1.
2. The derivative of the sum of two terms: (f + w) '= f'w + fw'.
3. Derivative of a logarithmic function: (log _a d) '= d / ln a * d. This formula applies to all kinds of logarithms.
4. Derivative of degree: (x ⁿ ) '= n * x ^n-1 . For example, (9x ² ) '= 9 * 2x = 18x.
5. Derivative of the sinusoidal function: (sin a) '= cos a. If the sin of the angle a is 0.5, then its derivative is √3 / 2.

Extremum points

We have already figured out how to find the minimum points, however, there is the concept of maximum points of a function. If the minimum indicates those points at which the function goes from the minus sign to the plus, then the maximum points are those points on the abscissa axis at which the derivative of the function changes from plus to the opposite - minus.

The maximum points can be found using the method described above, only it should be taken into account that they denote those areas where the function begins to decrease, that is, the derivative will be less than zero.

In mathematics, it is customary to generalize both concepts, replacing them with the phrase "points of extrema." When asked to determine these points in the task, this means that it is necessary to calculate the derivative of this function and find the minimum and maximum points.