The rotation figures in geometry are given special attention in the study of their characteristics and properties. One of them is a truncated cone. This article aims to answer the question of what formula can be used to calculate the area of a truncated cone.
What figure will we talk about?
Before describing the area of a truncated cone, it is necessary to give an exact geometric definition of this figure. Truncated is a cone that results from the plane cutting off the vertices of a regular cone. In this definition, a number of nuances should be emphasized. First, the section plane must be parallel to the plane of the base of the cone. Secondly, the original figure should be a circular cone. Of course, this can be an elliptical, hyperbolic and other kind of figure, but in this article we restrict ourselves to considering only a circular cone. The latter is shown in the figure below.
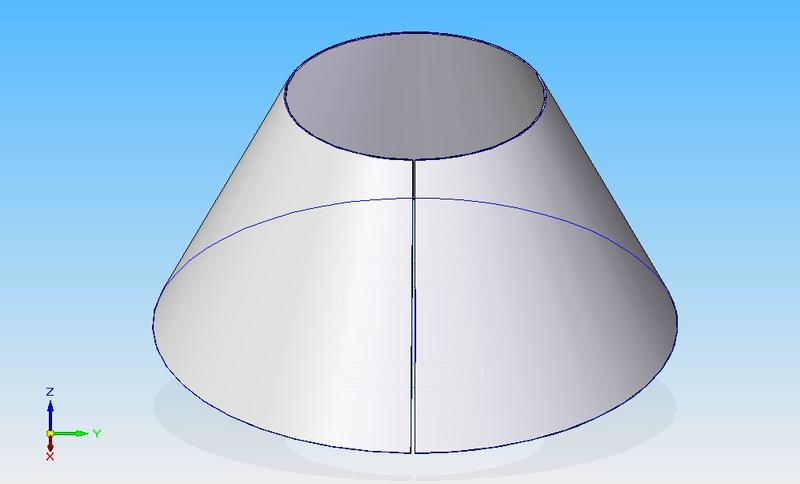
It is easy to guess that it can be obtained not only by means of a section by a plane, but also by a rotation operation. To do this, take the trapezoid, which has two right angles, and rotate it around the side that is adjacent to these right angles. As a result, the trapezoid bases will become the radii of the bases of the truncated cone, and the side inclined side of the trapezoid will describe the conical surface.
Shape Sweep
Considering the surface area of a truncated cone, it is useful to bring its scan, that is, the image of the surface of a volumetric figure on a plane. Below is a scan of the figure under study with arbitrary parameters.
It can be seen that the area of the figure is formed by three components: two circles and one truncated circular segment. Obviously, to determine the desired area, it is necessary to add up the area of all the named figures. We will solve this problem in the next paragraph.
Truncated cone area
To make it easier to understand the following reasoning, we introduce the following notation:
- r1, r2 are the radii of the large and small bases, respectively;
- h is the height of the figure;
- g is the generatrix of the cone (the length of the inclined side of the trapezoid).
The base area of the truncated cone is easy to calculate. We write the corresponding expressions:
S o1 = pi * r 1 2 ;
S o2 = pi * r 2 2 .
The area of a circular segment is somewhat more difficult to determine. If we imagine that the center of this circular sector is not cut, then its radius will be equal to G. It is not difficult to calculate it if we consider the corresponding similar rectangular triangles of the cone. It is equal to:
G = r 1 * g / (r 1 -r 2 ).
Then the area of the whole circular sector, which is built on a radius G and which rests on an arc of length 2 * pi * r 1 , will be equal to:
S 1 = pi * r 1 * G = pi * r 1 2 * g / (r 1 -r 2 ).
Now we determine the area of the small circular sector S 2 , which will need to be subtracted from S 1 . It is equal to:
S 2 = pi * r 2 * (G - g) = pi * r 2 * (r 1 * g / (r 1 -r 2 ) - g) = pi * r 2 2 * g / (r 1 -r 2 )
The area of the conical truncated surface S b is equal to the difference S 1 and S 2 . We get:
S b = S 1 - S 2 = pi * r 1 2 * g / (r 1 -r 2 ) - pi * r 2 2 * g / (r 1 -r 2 ) = pi * g * (r 1 + r 2 ).
Despite somewhat cumbersome calculations, we got a fairly simple expression for the area of the side surface of the figure.
Adding the area of the bases and S b , we come to the formula for the area of the truncated cone:
S = S o1 + S o2 + S b = pi * r 1 2 + pi * r 2 2 + pi * g * (r 1 + r 2 ).
Thus, in order to calculate the S value of the studied figure, it is necessary to know its three linear parameters.
Task example
A circular straight cone with a radius of 10 cm and a height of 15 cm was cut off by a plane so that a regular truncated cone was obtained. Knowing that the distance between the bases of the truncated figure is 10 cm, it is necessary to find the surface area.
To use the formula for the area of a truncated cone, it is necessary to find its three parameters. One we know:
r 1 = 10 cm.
The other two are easy to calculate if you look at similar triangles rectangular, which are obtained as a result of the axial section of the cone. Taking into account the conditions of the problem, we obtain:
r 2 = 10 * 5/15 = 3.33 cm.
Finally, the guide of the truncated cone g will be equal to:
g = √ (10 2 + (r 1 -r 2 ) 2 ) = 12.02 cm.
Now we can substitute the quantities r 1 , r 2 and g in the formula for S:
S = pi * r 1 2 + pi * r 2 2 + pi * g * (r 1 + r 2 ) = 851.93 cm 2 .
The desired surface area of the figure is approximately 852 cm 2 .